Rozwiązanie
Wyznaczamy najpierw dziedzinę nierówności \(\displaystyle{\textrm{log}_{x}(x^{3}-\displaystyle\frac{1}{4}\ x) \leq 1},\) dokonując założeń:
\[ \begin{array}{l}
x^{3}-\displaystyle\frac{1}{4}\ x >0 \ \wedge \ x>0 \ \wedge \ x\neq 1\\
x(x^{2}-\displaystyle\frac{1}{4}\ )>0 \ \wedge \ x>0 \ \wedge \ x\neq 1\\
x(x-\displaystyle\frac{1}{2}\ )(x+\displaystyle\frac{1}{2}\ )>0 \ \wedge \ x>0 \ \wedge \ x\neq 1
\end{array}\]
Wykonujemy rysunek, aby rozwiązać nierówność. Na osi zaznaczamy również pozostałe założenia i odczytujemy dziedzinę nierówności.
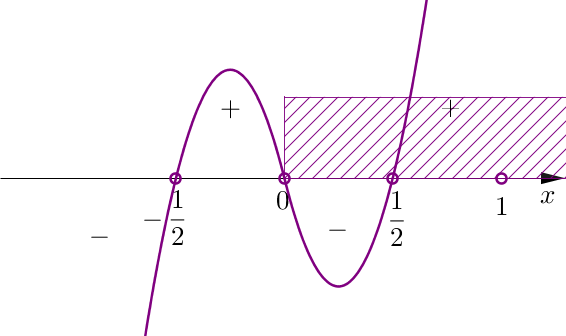
Zatem \[D=\left ( \displaystyle\frac{1}{2};\infty \right ) \setminus \left \{ 1 \right \}.\]
Nierówność rozwiązujemy rozbijając dziedzinę na dwa przypadki (od tego jaka jest wartość \(x\) zależy, czy opuszczamy logarytmy zmieniając czy nie zmieniając znaku nierówności na przeciwny).
\(1^{0}.\) Dla \(x\in (\displaystyle\frac{1}{2}\ ;1)\) mamy:
\[ \begin{array}{l}
\large{\textrm{log}_{x}(x^{3}-\displaystyle\frac{1}{4}\ x)\leq \textrm{log}_{x}x}\\
\large{x^{3}-\displaystyle\frac{1}{4}x \geq x}\\
\large{x^{3}-\displaystyle\frac{1}{4}x -x\geq 0}\\
\large{x^{3}-\displaystyle\frac{5}{4}x\geq 0}\\
\large{x(x^{2}-\displaystyle\frac{5}{4}\ )\geq 0}\\
\large{x(x-\displaystyle\frac{\sqrt{5}}{2}\ )(x+\displaystyle\frac{\sqrt{5}}{2}\ )\geq 0}\\
\large{x=0 \ \ \vee \ \ x=\displaystyle\frac{\sqrt{5}}{2} \ \ \vee \ \ x=-\displaystyle\frac{\sqrt{5}}{2}}
\end{array}\]
Opuściliśmy logarytmy zmieniając znak nierówności na przeciwny, gdyż założyliśmy, że podstawa logarytmu mieści się w przedziale między \(\displaystyle\frac{1}{2}\) a \(1.\)
Rysujemy wykres wielomianu znajdującego się po lewej stronie nierówności i odczytujemy dla jakich argumentów wielomian ten przyjmuje wartości większe lub równe zero.
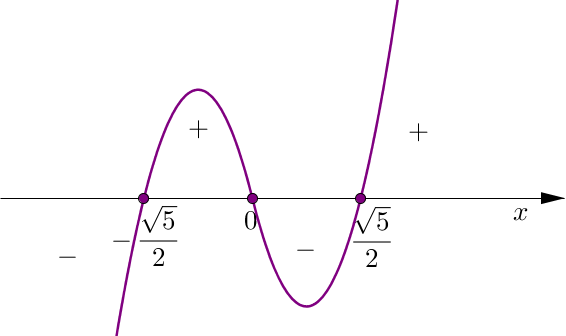
Zatem \[x\in \left \langle - \displaystyle\frac{\sqrt{5}}{2};0\right \rangle\cup \left \langle \displaystyle\frac{\sqrt{5}}{2};\infty \right ).\]
W przekroju z założeniem otrzymamy:
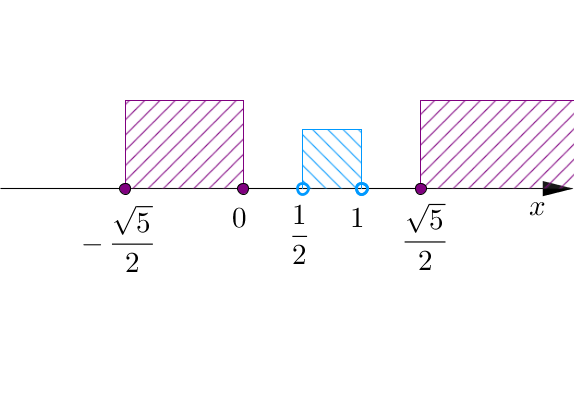
Widać, że nie ma liczb spełniających założenie, dla których wielomian przyjmuje wartości nieujemne. Zatem \[x\in \varnothing .\]
\(2^{0}.\) Dla \(x \in \left ( 1;\infty \right )\) mamy:
\[ \begin{array}{l}
\large{\textrm{log}_{x}(x^{3}-\displaystyle\frac{1}{4}\ x)\leq \textrm{log}_{x}x}\\
\large{x^{3}-\displaystyle\frac{1}{4}x \leq x}\\
\large{x^{3}-\displaystyle\frac{1}{4}x -x \leq 0}\\
\large{x^{3}-\displaystyle\frac{5}{4}x \leq 0}\\
\large{x(x^{2}-\displaystyle\frac{5}{4}\ ) \leq 0}\\
\large{x(x-\displaystyle\frac{\sqrt{5}}{2}\ )(x+\displaystyle\frac{\sqrt{5}}{2}\ ) \leq 0}\\
\large{x=0 \ \ \vee \ \ x=\displaystyle\frac{\sqrt{5}}{2} \ \ \vee \ \ x=-\displaystyle\frac{\sqrt{5}}{2}}
\end{array}\]
Opuszczając logarytmy nie zmieniamy znaku nierówności na przeciwny, gdyż w założeniu podstawa logarytmu należy do przedziału \(\left ( 1;\infty \right ).\) Odczytujemy z wykresu dla jakich argumentów wielomian po lewej stronie nierówności przyjmuje wartości mniejsze lub równe zero.

Mamy więc \[x\in \left ( -\infty ;- \displaystyle\frac{\sqrt{5}}{2}\right \rangle \cup \left \langle 0;\displaystyle\frac{\sqrt{5}}{2} \right \rangle.\]
Częścią wspólną z założeniem będzie zbiór \[\left (1;\displaystyle\frac{\sqrt{5}}{2} \right \rangle.\]
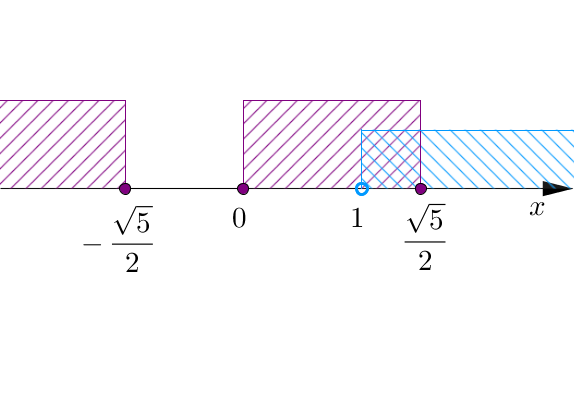
Aby do końca rozwiązać daną nierówność należy zsumować rozwiązania z obu przypadków. Ponieważ w pierwszym przypadku nie było liczb spełniających nierówność, zatem rozwiązaniem równania są liczby z przedziału \(\left (1;\displaystyle\frac{\sqrt{5}}{2} \right \rangle.\)

