Zadanie 7.1.1
  1. Analiza matematyczna 1
  2. 7. Badanie przebiegu zmienności funkcji
  3. 7.1 Monotoniczność i ekstrema lokalne
  4. Zadanie 7.1.1

 Polecenie

Znajdź przedziały monotoniczności podanych funkcji.

 Wskazówki

Twierdzenie (warunki wystarczające monotoniczności funkcji)

Jeżeli funkcja \(f,\) dla dowolnego \(x\) z przedziału \(I,\) spełnia warunek:
  • \(f'(x)=0,\) to jest stała na przedziale \(I,\)
  • \(f'(x)\gt 0,\) to jest rosnąca (ściśle rosnąca) na przedziale \(I,\)
  • \(f'(x) \geqslant 0,\) to jest niemalejąca (słabo rosnąca) na przedziale \(I,\)
  • \(f'(x)\lt 0,\) to jest malejąca (ściśle malejąca) na przedziale \(I,\)
  • \(f'(x) \leqslant 0,\) to jest nierosnąca (słabo malejąca) na przedziale \(I.\)
Uwaga
Jeżeli \(f'(x)\geqslant  0\) dla każdego \(x\in I,\) przy czym ta pochodna jest równa zero tylko dla skończonej liczby punktów tego przedziału, to funkcja \(f\) jest rosnąca na \(I.\) Podobnie jest dla pozostałych warunków.

 Funkcja 1

\({\displaystyle f(x)=\frac{2x}{5+x^{2}}}\)

 Rozwiązanie

Algorytm
Wyznaczanie przedziałów monotoniczności odbywa się w trzech krokach:
1. Wyznaczenie dziedziny funkcji \(f.\)
2. Obliczenie pochodnej funkcji \(f.\)
3. Wyznaczenie podzbiorów dziedziny funkcji \(f,\) w których pierwsza pochodna jest dodatnia/ujemna.
Zaczynamy od wyznaczenia dziedziny funkcji \({\displaystyle f(x)=\frac{2x}{5+x^{2}}}.\) Ponieważ w mianowniku mamy wyrażenie zawsze różne od zera, zatem dziedziną funkcji \(f\) jest zbiór liczb rzeczywistych \(D_{f}=\mathbb{R}.\)
Liczymy pochodną funkcji \(f:\)
\[f'(x)=\frac{2(5+x^{2})-2x\cdot 2x}{(5+x^{2})^{2}}=\frac{10-2x^{2}}{(5+x^{2})^{2}}\]
Rozwiązujemy nierówność \({\displaystyle \frac{10-2x^{2}}{(5+x^{2})^{2}}\gt 0},\) aby wyznaczyć przedziały monotoniczności. Oczywiście dostaniemy w ten sposób przedziały argumentów, dla których pochodna przyjmuje zarówno wartości dodatnie jak i ujemne, więc znak \(\gt, \ \lt\) w nierówności nie ma znaczenia.
\[ \begin{array}{l}
{\displaystyle \frac{10-2x^{2}}{(5+x^{2})^{2}} \gt 0}\\
(10-2x^{2})(5+x^{2})^{2} \gt 0\\
10-2x^{2}=0  \ \ \vee  \ \ (5+x^{2})^{2}=0\\
2(5-x^{2})=0, \ \ \underset{x\in \mathbb{R}}{\huge \forall } (5+x^{2})^{2} \gt 0\\
(\sqrt{5}-x)(\sqrt{5}+x)=0\\
x=\sqrt{5} \ \vee \ x=-\sqrt{5}
\end{array}\]
Rysujemy wykres wielomianu, aby odczytać przedziały monotoniczności. (Wykresy pomocnicze wielomianów oraz sposób rozwiązywania nierówności wymiernych omówione są w rozdziale 3. Funkcje)
_rysunek_7.1.1.2
Jak widać na rysunku funkcja \(f:\)
  • jest malejąca dla \(x\in \left ( -\infty ;-\sqrt{5} \right ),\) gdyż \(f'(x) \lt 0,\)
  • jest rosnąca dla \(x\in \left (-\sqrt{5};\sqrt{5} \right ), \) gdyż \(f'(x) \gt 0,\)
  • jest malejąca dla \(x\in \left ( \sqrt{5}; \infty \right ),\) gdyż \(f'(x) \lt 0.\)

 Odpowiedź

Funkcja \(f\) jest
  • malejąca dla \(x\in \left ( -\infty ;-\sqrt{5} \right ),\)
  • rosnąca dla \(x\in \left (-\sqrt{5};\sqrt{5} \right ),\)
  • malejąca dla \(x\in \left ( \sqrt{5}; \infty \right ).\)

 Funkcja 2

\(g(x)=\ln(x^{2}-1)\)

 Rozwiązanie

Ponieważ w funkcji \(g(x)=\ln(x^{2}-1)\) argumentem logarytmu jest \(x^{2}-1,\) zatem przy wyznaczaniu dziedziny musimy założyć, że \(x^{2}-1\) jest liczbą dodatnią. Rozwiązujemy zatem nierówność \(x^{2}-1\gt 0.\)
\[ \begin{array}{l}
x^{2}-1 \gt 0\\
(x-1)(x+1)\gt 0\\
x=1 \ \vee x=-1
\end{array}\]
Szkicujemy wykres 
_rysunek_7.1.1.3
i wyznaczamy dziedzinę.
\[x\in \left ( -\infty;-1 \right )\cup \left ( 1;\infty \right )\]
Zatem \(D_{f}=\left ( -\infty;-1 \right )\cup \left ( 1;\infty \right ).\)
Wyznaczamy pochodną funkcji \(f(x)=\ln(x^{2}-1).\)
\[{\displaystyle f'(x)= \frac{1\cdot 2x}{x^{2}-1}=\frac{2x}{x^{2}-1}},\]
oraz wyznaczamy przedziały monotoniczności rozwiązując nierówność
\[ \begin{array}{l}
{\displaystyle \frac{1\cdot 2x}{x^{2}-1}\gt 0}\\
2x(x^{2}-1)\gt 0\\
2x(x+1)(x-1)\gt 0\\
x=0 \ \vee \ x=-1 \ \vee \ x=1
\end{array}\]
i odczytując z wykresu
_rysunek_7.1.1.5
uwzględniając dziedzinę, czyli sumę zbiorów \(\left ( -\infty;-1 \right )\cup \left ( 1;\infty \right ).\)
  • \(f\) jest funkcją rosnącą, jeśli \( x\in \left ( 1;\infty \right ),\)
  • \(f\) jest funkcją malejącą, jeśli \(x\in \left ( -\infty;-1 \right ).\)

 Odpowiedź

\[ \begin{array}{l}
f \nearrow   \ \ \Leftrightarrow \ \ x\in \left ( 1;\infty \right )\\
f  \searrow  \ \ \Leftrightarrow \ \ x\in \left ( -\infty;-1 \right )
\end{array}\]

 Funkcja 3

\(f(x)=x^{2}e^{-2x}\)

 Rozwiązanie

 Krok 1

W pierwszym kroku wyznaczamy dziedzinę funkcji \(f(x)=x^{2}e^{-2x}.\) Wybierz właściwą odpowiedź.

\[D_{f}=\mathbb{R}\setminus \left \{ 0 \right \}\]

Odpowiedź nieprawidłowa

\[D_{f}=\mathbb{R}\]

Odpowiedź prawidłowa

\[D_{f}=\mathbb{R}_{+}\]

Odpowiedź nieprawidłowa

 Krok 2

W kolejnym kroku, dla \(x \in \mathbb{R}\), wyznaczamy pochodną funkcji \(f(x)=x^{2}e^{-2x}.\) Wybierz właściwą odpowiedź.

\(f'(x)=(2x-2x^{2})e^{-2x}\)

Odpowiedź prawidłowa

\(f'(x)=2x^{2}e^{-2x}\)

Odpowiedź nieprawidłowa

\(f'(x)=(4x-2x^{2})e^{-2x}\)

Odpowiedź nieprawidłowa

 Krok 3

Rozwiązujemy nierówność \(f'(x)\gt 0\) i wyznaczamy przedziały monotoniczności. Wybierz właściwy wykres.

_rysunek_7.1.1.6

Odpowiedź nieprawidłowa

_rysunek_7.1.1.7

Odpowiedź prawidłowa

_rysunek_7.1.1.8

Odpowiedź nieprawidłowa
Obliczenia
Pochodna: \(f'(x)=2xe^{-2x}+x^{2}e^{-2x}\cdot (-2)=(2x-2x^{2})e^{-2x}.\)
Rozwiązanie nierówności:
\[ \begin{array}{l}
(2x-2x^{2})e^{-2x}\gt 0\\
2x(1-x)e^{-2x} \gt 0\\
x=0 \ \vee \ x=1, \ \ \underset{x\in \mathbb{R}}{\huge \forall } e^{-2x} \gt 0
\end{array}\]
_rysunek_7.1.1.7

\[ \begin{array}{l}
f'(x)\gt 0 \ \Leftrightarrow \ x\in \left ( 0;1 \right )\\
f'(x)\lt 0 \ \Leftrightarrow \ x\in \left ( -\infty; 0 \right )\\
f'(x)\lt 0 \ \Leftrightarrow \ x\in \left ( 1; \infty \right )
\end{array}\]

 Odpowiedź

\[ \begin{array}{l}
f \nearrow \ \Leftrightarrow \ x\in \left ( 0;1 \right )\\
f \searrow \ \Leftrightarrow \ x\in \left ( -\infty; 0 \right )\\
f \searrow \ \Leftrightarrow \ x\in \left ( 1; \infty \right )
\end{array}\]

 Polecenie

Znajdź przedziały monotoniczności podanych funkcji.

 Funkcja 1

\({\displaystyle f(x)=\frac{\sqrt{x}}{\ln x}}\)

 Odpowiedź

\[ \begin{array}{l}
f \searrow \ \Leftrightarrow \ x\in \left ( 0;1 \right )\\
f \searrow \ \Leftrightarrow \ x\in \left ( 1;e^{2} \right )\\
f \nearrow \ \Leftrightarrow \ x\in \left ( e^{2};\infty \right )
\end{array}\]

 Rozwiązanie

Dziedzina funkcji \(f:\)
\[x\geqslant 0, \ \ x \gt 0, \ \ \ln x\neq 0 \ \Leftrightarrow \ x\neq 1\]
Zatem \(D_{f}=\mathbb{R}_{+}\setminus \left \{ 1 \right \}.\)
\[ \begin{array}{l}
{\displaystyle f(x)=\frac{\sqrt{x}}{\ln x}}\\
{\displaystyle f'(x)=\frac{\frac{1}{2\sqrt{x}}\ln x-\sqrt{x}\cdot \frac{1}{x}}{\ln^{2}x}=
\frac{\frac{\ln x}{2\sqrt{x}}-\frac{1}{\sqrt{x}}}{\ln^{2}x}=
\frac{\frac{\ln x}{2}-1}{\sqrt{x}\ln^{2}x}}\\
{\displaystyle f'(x)\gt 0 \ \Leftrightarrow  \ \frac{\frac{\ln x}{2}-1}{\sqrt{x}\ln^{2}x}\gt 0}\\
{\displaystyle \sqrt{x}\ln^{2}x(\frac{\ln x}{2}-1) \gt 0}\\
{\displaystyle \sqrt{x} =0 \ \ \vee \ \ \ln^{2}x =0 \ \ \vee \ \ \frac{\ln x}{2}=1}\\
{\displaystyle x =0 \ \ \vee \ \ \ln x =0 \ \ \vee \ \ \ln x=2}\\
{\displaystyle x =0 \ \ \vee \ \ x =1 \textrm {- p. 2-kr.} \ \ \vee \ \ \ln x=2}\\
{\displaystyle x =0 \ \ \vee \ \ x =1 \textrm {- p. 2-kr.} \ \ \vee \ \ x=e^{2}}\\
\end{array}\]
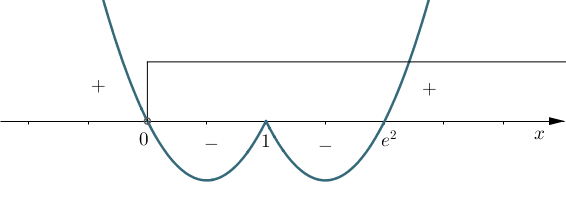
_rysunek_7.1.1.9

Zatem uwzględniając dziedzinę \(x\gt 0,\ x\neq 1\) mamy:
\[ \begin{array}{l}
f \searrow \ \Leftrightarrow \ x\in \left ( 0;1 \right )\\
f \searrow \ \Leftrightarrow \ x\in \left ( 1;e^{2} \right )\\
f \nearrow \ \Leftrightarrow \ x\in \left ( e^{2};\infty \right )
\end{array}\]

 Funkcja 2

\({\displaystyle f(x)=\frac{x^{2}}{2-x}}\)

 Odpowiedź

\[ \begin{array}{l}
f \searrow \ \Leftrightarrow \ x\in \left ( -\infty;0 \right )\\
f \nearrow \ \Leftrightarrow \ x\in \left ( 0;2 \right )\\
f \nearrow \ \Leftrightarrow \ x\in \left ( 2;4 \right )\\
f \searrow \ \Leftrightarrow \ x\in \left ( 4;\infty \right )
\end{array}\]

 Rozwiązanie

Dziedziną funkcji \(f\) jest zbiór \(D_{f}=\mathbb{R}\setminus \left \{ 2 \right \}.\)
Liczymy pochodną, rozwiązujemy nierówność wymierną i wyznaczamy przedziały monotoniczności funkcji \(f.\)
\[ \begin{array}{l}
{\displaystyle f(x)=\frac{x^{2}}{2-x}}\\
{\displaystyle f'(x)=\frac{2x(2-x)-x^{2}\cdot (-1)}{(2-x)^{2}}=\frac{4x-2x^{2}+x^{2}}{(2-x)^{2}}=
\frac{4x-x^{2}}{(2-x)^{2}}}\\
{\displaystyle \frac{4x-x^{2}}{(2-x)^{2}}\gt 0}\\
{\displaystyle \left (4x-x^{2}  \right )(2-x)^{2}\gt 0}\\
x(4-x)(2-x)^{2} \gt 0\\
x=0  \ \ \vee \ \ x=4 \ \ \vee \ \  x=2 \textrm{ - p. 2-kr.} \\
\end{array}\]
_rysunek_7.1.1.10

Zatem
\[ \begin{array}{l}
f \searrow \ \Leftrightarrow \ x\in \left ( -\infty;0 \right )\\
f \nearrow \ \Leftrightarrow \ x\in \left ( 0;2 \right )\\
f \nearrow \ \Leftrightarrow \ x\in \left ( 2;4 \right )\\
f \searrow \ \Leftrightarrow \ x\in \left ( 4;\infty \right )
\end{array}\]