Korzystając z cechy podobieństwa kąt-kąt-kąt układamy proporcję sugerując się powyższym rysunkiem.
\[ \begin{array}{l}
{\displaystyle \frac{x}{l}=\frac{R}{r}}\\
rx=lR\\
rx=R\sqrt{(x+R)^{2}+r^{2}} \ \ /()^{2}\\
r^{2}x^{2}=R^{2}\left ( (x+R)^{2}+r^{2} \right )\\
r^{2}x^{2}=R^{2}(x+R)^{2}+R^{2}r^{2}\\
r^{2}x^{2}-R^{2}r^{2}=R^{2}(x+R)^{2}\\
r^{2}\left (x^{2}-R^{2}\right )=R^{2}(x+R)^{2}\\
{\displaystyle r^{2}=\frac{R^{2}(x+R)^{2}}{x^{2}-R^{2}}}
\end{array}\]
Można skrócić wyrażenie, redukując wyrazy podobne. Wcześniej jednak określimy dziedzinę danego wyrażenia. Aby mieć po prawej stronie liczbę dodatnią, musi być spełnione założenie:
\(x^{2}-R^{2}\gt 0.\) Zatem pomożemy sobie wykresem (pierwiastki równania to \(x=-R\) oraz \(x=R\)).
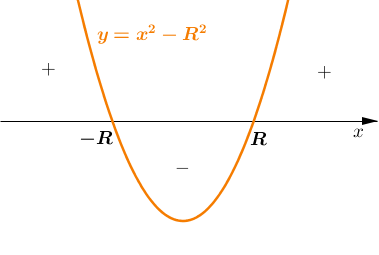
Dziedziną wyrażenia są więc wszystkie liczby rzeczywiste większe od \(R.\) (\(x\gt R\))
Skracamy wyrażenie algebraiczne, korzystając ze wzoru skróconego mnożenia na różnicę kwadratów oraz rozpisując kwadrat wyrażenia \(x+R\) jako iloczyn dwóch tych samych czynników.
\[ \begin{array}{l}
{\displaystyle r^{2}=\frac{R^{2}\left (x+R \right )\left ( x+R \right )}{\left (x-R\right )\left (x+R\right )}}\\
{\displaystyle r^{2}=\frac{R^{2}\left (x+R \right )\cancel{\left ( x+R \right )}}{\left (x-R\right )\cancel{\left (x+R\right )}}}\\
\end{array}\]
Mając dane \({\displaystyle r^{2}=\frac{R^{2}\left (x+R \right )}{x-R}} \) oraz \( H=x+R,\) podstawiamy do wzoru na objętość stożka i otrzymujemy funkcję zmiennej \(x.\)
\[V(x)=\frac{1}{3}\pi \frac{R^{2}\left (x+R \right )}{x-R}\cdot (x+R)=\frac{\pi R^{2}\left (x+R \right )^{2}}{3\left (x-R \right )}.\]
Liczymy pochodną funkcji \(V.\)
\[ \begin{array}{l}
{\displaystyle V'(x)=\frac{\pi R^{2}}{3}\cdot \frac{2\left ( x+R \right )\cdot 1\cdot \left ( x-R \right )-\left ( x+R \right )^{2}\cdot 1}{\left ( x-R \right )^{2}}=}\\
{\displaystyle =\frac{\pi R^{2}}{3}\cdot \frac{2\left ( x^{2}-R^{2} \right )- \left (x^{2}+2xR+ R^{2} \right )}{\left ( x-R \right )^{2}}=}\\
{\displaystyle =\frac{\pi R^{2}}{3}\cdot \frac{2x^{2}-2R^{2}- x^{2}-2xR- R^{2}}{\left ( x-R \right )^{2}}=}\\
{\displaystyle =\frac{\pi R^{2}}{3}\cdot \frac{x^{2}-2xR-3R^{2} }{\left ( x-R \right )^{2}}}
\end{array}\]
Aby wyznaczyć znak pochodnej rozwiązujemy równanie i rysujemy wykres:
\[ \begin{array}{l}
x^{2}-2xR-3R^{2}=0\\
\Delta =(-2R)^{2}-4\cdot 1\cdot (-3R^{2})=4R^{2}+12R^{2}=16R^{2}, \ R \gt 0\\
\sqrt{\Delta }=4R\\
{\displaystyle x_{1}=\frac{2R-4R}{2}=-R}\\
{\displaystyle x_{2}=\frac{2R+4R}{2}=3R}\\
\end{array}\]
Zatem dla \(x=3R\) objętość stożka będzie najmniejsza \(V _{\textrm{min}}\), gdyż pochodna zmienia znak z ujemnej na dodatnią, czyli funkcja \(V(x)\) zmienia się z malejącej na rosnącą. Osiąga więc minimum w punkcie \(x=3R.\)
Wówczas: \(H=3R+R=4R.\)

