Zadanie 3.5.2
  1. Analiza matematyczna 1
  2. 3. Funkcje
  3. 3.5 Funkcje trygonometryczne i cyklometryczne
  4. Zadanie 3.5.2

 Polecenie

Uzasadnij tożsamości trygonometryczne.

 Wskazówki

Definicje funkcji trygonometrycznych
Niech \(\alpha\) będzie miarą łukową (wyrażoną w radianach) kąta uogólnionego skierowanego, którego pierwszym ramieniem (początkowym) jest oś \(OX\) a drugim ramieniem (końcowym) jest półprosta o początku w punkcie \(O(0,0)\) przechodząca przez punkt \(P(x,y),\) dla \((x, y )\neq (0,0).\)
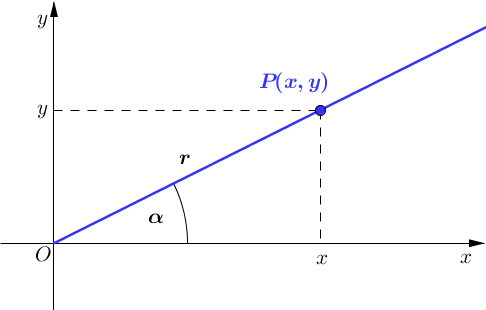
Rysunek 3.5.2.1

Przy takich oznaczeniach definiujemy wartości funkcji trygonometrycznych nastepująco:
\[\begin{array}{l}
\large{\sin \alpha =\displaystyle\frac{y}{r}}\\
\large{\cos \alpha = \displaystyle\frac{x}{r}}\\
\large{\operatorname{tg}{\alpha} =\displaystyle\frac{y}{x}}\\
\large{\operatorname{ctg}{\alpha}=\displaystyle\frac{x}{y}}.
\end{array}\]
Podstawowe związki między funkcjami trygonometrycznymi
\[ \begin{array}{l}
\large{\sin^{2}x+\cos^{2}x=1,\ \  x\in \mathbb{R}}\\
\large{\operatorname{tg}{x}=\displaystyle\frac{\sin x}{\cos x}, \ \ x\neq (2k+1)\frac{\pi }{2},\  k\in \mathbb{Z}}\\
\large{\operatorname{ctg}{x}=\displaystyle\frac{\cos x}{\sin x},\ \  x\neq k\pi,\  k\in \mathbb{Z}}\\
\large{\operatorname{tg}{x} \cdot \operatorname{ctg}{x}=1,\ \  x\neq k\cdot \displaystyle\frac{\pi }{2}, \ k\in \mathbb{Z}}.
\end{array}\]
Funkcje trygonometryczne sumy i różnicy kątów
Dla dowolnych \(x, y\in \mathbb{R}\) prawdziwe są następujące wzory:
\[ \begin{array}{l}
\large{\sin (x+y)=\sin x \cos y+ \cos x \sin y}\\
\large{\sin (x-y)=\sin x \cos y- \cos x \sin y}\\
\large{\cos (x+y)=\cos x \cos y- \sin x \sin y}\\
\large{\cos (x-y)=\cos x \cos y+ \sin x \sin y}.
\end{array}\]
Na podstawie tych wzorów można wyprowadzić również wzory na tangens i cotangens sumy i różnicy kątów:
\[ \begin{array}{l}
\large \operatorname{tg}{(x+y)}=\displaystyle\frac{\operatorname{tg}{x}+\operatorname{tg}{y}}{1-\operatorname{tg}{x} \cdot \operatorname{tg}{y}}\\
\large \operatorname{ctg}{(x+y)}=\displaystyle\frac{\operatorname{ctg}{x}\cdot \operatorname{ctg}{y-1}}{\operatorname{ctg}{y}+\operatorname{tg}{x}}\\
\large \operatorname{tg}{(x-y)}=\displaystyle\frac{\operatorname{tg}{x}-\operatorname{tg}{y}}{1+\operatorname{tg}{x}\cdot \operatorname{tg}{y}}\\
\large \operatorname{ctg}{(x-y)}=\displaystyle\frac{\operatorname{ctg}{x}\cdot \operatorname{ctg}{y}+1}{\operatorname{ctg}{y}-\operatorname{tg}{x}}.
\end{array}\]
Sumy i różnice funkcji trygonometrycznych
Dla dowolnych \(x, y\in \mathbb{R}\) prawdziwe są następujące wzory:
\[ \begin{array}{l}
\large{\sin x+\sin y=2\sin \displaystyle\frac{x+y}{2}\cos \displaystyle\frac{x-y}{2}},\\
\large{\sin x-\sin y=2\cos \displaystyle\frac{x+y}{2}\sin \displaystyle\frac{x-y}{2}},\\
\large{\cos x+\cos y=2\cos \displaystyle\frac{x+y}{2}\cos \displaystyle\frac{x-y}{2}},\\
\large{\cos x-\cos y=-2\sin \displaystyle\frac{x+y}{2}\sin \displaystyle\frac{x-y}{2}}.
\end{array}\]
Na podstawie tych wzorów można wyprowadzić również wzory na sumy i różnice tangensów i cotangensów.
\[ \begin{array}{l}
\large{\operatorname{tg}{x}+\operatorname{tg}{y}=\displaystyle\frac{\sin(x+y)}{\cos x \cos y},}\\
\large{\operatorname{tg}{x}-\operatorname{tg}{y}=\displaystyle\frac{\sin(x-y)}{\cos x \cos y},}\\
\large{\operatorname{ctg}{x}+\operatorname{ctg}{y}=\displaystyle\frac{\sin(x+y)}{\sin x \sin y},}\\
\large{\operatorname{ctg}{x}-\operatorname{ctg}{y}=-\displaystyle\frac{\sin(x-y)}{\sin x \sin y}.}
\end{array}\]
Funkcje trygonometryczne podwojonego kąta
Dla dowolnego \(x\in \mathbb{R}\) prawdziwe są następujące wzory:
\[ \begin{array}{l}
\large{\sin 2x=2\sin x \cos x},\\
\large{\cos 2x=\cos^{2}x-\sin^{2}x=2\cos^{2}x-1=1-2\sin^{2}x},\\
\large{\operatorname{tg}{2x}=\displaystyle\frac{2\operatorname{tg}{x}}{1-\operatorname{tg}^{2}{x}}},\\
\large{\operatorname{ctg}{2x}=\displaystyle\frac{\operatorname{ctg}^{2}{x-1}}{2\operatorname{ctg}{x}}}.
\end{array}\]
Funkcje trygonometryczne kąta połówkowego
Dla dowolnego \(x\in \mathbb{R}\) prawdziwe są następujące wzory:
\[ \begin{array}{l}
\large{\sin^{2}\displaystyle \frac{x}{2}=\displaystyle\frac{1-\cos x}{2}},\\
\large{\cos^{2}\displaystyle \frac{x}{2}=\displaystyle\frac{1+\cos x}{2}},\\
\large{\operatorname{tg}{\displaystyle\frac{x}{2}}=\displaystyle\frac{1-\cos x}{\sin x}=\displaystyle\frac{\sin x}{1+\cos x}},\\
\large{\operatorname{ctg}{\displaystyle \frac{x}{2}}=\displaystyle\frac{\sin x}{1-\cos x}=\displaystyle\frac{1+\cos x}{\sin x}}.
\end{array}\]

 Tożsamość 1

\(2\operatorname{tg}{x}+\operatorname{ctg}{x}= \displaystyle\frac{2(1+\sin^{2}x)}{\sin 2x}\)

 Rozwiązanie

Przekształcamy lewą stronę równania (w niektórych przypadkach można zacząć przekształcenia od prawej strony równania).
\[
\large{\begin{matrix}\begin{array}{l}
L = 2\operatorname{tg}{x}+\operatorname{ctg}{x}=  & \textrm{rozpisujemy tangens i cotangens} \\
\displaystyle \frac{2\sin x}{\cos x}+\displaystyle \frac{\cos x}{\sin x}= & \textrm{sprowadzamy do wspólnego mianownika} \\
\displaystyle \frac{\color{orange}{2 \sin^{2}x}+\cos ^{2}x}{\sin x \cos x}= & \textrm{zapisujemy iloczyn jako sumę kwadratów dwóch sinusów} \\
\displaystyle \frac{\sin^{2}x+\color{orange}{\sin^{2}x+\cos ^{2}x}}{\sin x \cos x}= & \textrm{można zauważyć, że dostaliśmy jedynkę trygonometryczną} \\
\displaystyle \frac{\sin^{2}x+\color{orange}{1}}{\sin x \cos x}= & \textrm{dopisujemy w mianowniku iloczyn liczb } \displaystyle\frac{1}{2}\cdot 2\\
\displaystyle \frac{\sin^{2}x+1}{\color{orange}{\displaystyle\frac{1}{2}\cdot 2} \sin x \cos x}=& \textrm{aby otrzymać wzór na sinus podwojonego kąta}\\
\displaystyle \frac{\sin^{2}x+1}{\displaystyle\frac{1}{2}\cdot \color{orange}{ 2 \sin x \cos x}}=& \textrm{korzystamy ze wzoru, a zamiast dzielić przez jedną drugą, mnożymy przez dwa}\\
\displaystyle \frac{2(\sin^{2}x+1)}{\sin 2x }=P. & \textrm{co należało udowodnić} \end{array}
\end{matrix}}
\]

 Tożsamość 2

\(\operatorname{tg}^{4}{x}-\operatorname{ctg}^{4}{x}=\displaystyle\frac{-16\cos 2x(1-\frac{1}{2}\sin^{2}2x)}{\sin^{4}2x}\)

 Rozwiązanie

W kolejnych krokach przekształcimy jedną ze stron tożsamości aby dojść do drugiej strony i udowodnić jej prawdziwość.

 Krok 1

Rozpisujemy lewą stronę równania.
W pierwszym kroku skorzystamy dwukrotnie ze wzoru skróconego mnożenia na  \(a^{2}-b^{2}=(a+b)(a-b)\) .
\[ \begin{array}{l}
L = \operatorname{tg}^{4}{x}-\operatorname{ctg}^{4}{x}=\\
(\operatorname{tg}^{2}{x}-\operatorname{ctg}^{2}{x})(\operatorname{tg}^{2}{x}+\operatorname{ctg}^{2}{x})=\\
(\operatorname{tg}{x}-\operatorname{ctg}{x})(\operatorname{tg}{x}+\operatorname{ctg}{x})(\operatorname{tg}^{2}{x}+\operatorname{ctg}^{2}{x})= \cdots
\end{array}\]

 Krok 2

W drugim kroku rozpisujemy tangens i cotangens za pomocą sinusów i cosinusów tego samego kąta korzystając z podstawowych związków między funkcjami trygonometrycznymi. Sprowadzamy ułamki do wspólnych mianowników.
\[ \begin{array}{l}
\cdots = \Big( \displaystyle\frac{\sin x}{\cos x}-\displaystyle\frac{\cos x}{\sin x} \Big) \Big( \displaystyle\frac{\sin x}{\cos x}+\displaystyle\frac{\cos x}{\sin x} \Big) \Big( \displaystyle\frac{\sin ^{2}x}{\cos^{2} x}+\displaystyle\frac{\cos^{2} x}{\sin^{2} x} \Big) =\\
\displaystyle\frac{\sin ^{2}x-\cos^{2}x}{\sin x\cos x}\cdot \displaystyle\frac{\sin^{2}x+\cos^{2}x}{\sin x\cos x}\cdot \displaystyle\frac{\sin^{4}x+\cos^{4}x}{\sin^{2}x\cos^{2}x} =\cdots
\end{array}\]

 Krok 3

W trzecim kroku w liczniku pierwszego ułamka wyłączamy minus, w liczniku drugiego ułamka korzystamy z jedynki trygonometrycznej. Aby skorzystać z wzoru na sinus podwojonego kąta, w mianownikach wszystkich trzech ułamków dopisujemy odpowiednie iloczyny.
\[ \begin{array}{l}
\cdots = \displaystyle\frac{-(\cos^{2}x-\sin ^{2}x)}{\sin x\cos x}\cdot \displaystyle\frac{1}{\sin x\cos x}\cdot \displaystyle\frac{\sin^{4}x+\cos^{4}x}{\sin^{2}x\cos^{2}x} =\\
\displaystyle\frac{-(\cos^{2}x-\sin ^{2}x)}{\displaystyle\frac{1}{2}\cdot 2\sin x\cos x}\cdot \displaystyle\frac{1}{\displaystyle\frac{1}{2}\cdot 2\sin x\cos x}\cdot \displaystyle\frac{\sin^{4}x+\cos^{4}x}{\displaystyle\frac{1}{4}\cdot 4\sin^{2}x\cos^{2}x} = \cdots 
\end{array}\]

 Krok 4

Następnie korzystamy ze wzoru na sinus podwojonego kąta oraz w liczniku pierwszego ułamka na cosinus podwojonego kąta. Ułamki z mianowników w wyniku mnożenia przez odwrotność weszły do licznika jako liczby całkowite. Mnożymy też przez siebie dwa pierwsze ułamki.
\[ \begin{array}{l}
\cdots =\displaystyle\frac{-2(\cos 2x)}{2\sin x\cos x}\cdot \displaystyle\frac{2}{2\sin x\cos x}\cdot \displaystyle\frac{4(\sin^{4}x+\cos^{4}x)}{4\sin^{2}x\cos^{2}x} =\\
\displaystyle\frac{-2\cos 2x}{\sin 2x}\cdot \displaystyle\frac{2}{ \sin 2x}\cdot \displaystyle\frac{4(\sin^{4}x+\cos^{4}x)}{\sin^{2}2x} =\\
\displaystyle\frac{-4\cos 2x}{\sin^{2} 2x}\cdot \displaystyle\frac{4(\sin^{4}x+\cos^{4}x)}{\sin^{2}2x} =\cdots
\end{array}\]

 Krok 5

W tym kroku rozpiszemy osobno licznik drugiego ułamka.
Korzystamy tutaj ze wzoru jedynkowego, później wyłączamy przed nawias wspólny czynnik dwóch ostatnich wyrazów i kolejny raz stosujemy wzór jedynkowy. Na końcu znaną nam już metodą korzystamy ze wzoru na sinus podwojonego kąta.
\(\sin^{4}x+\cos^{4}x=(\color{orange}{\sin^{2}x})^{2}+\cos^{4}x=(\color{orange}{1-\cos^{2}x})^{2}+\cos^{4}x
=1-2\cos^{2}x+\cos^{4}x+\cos^{4}x=\\
1-2\cos^{2}x+2\cos^{4}x=1+2\cos^{4}x-2\cos^{2}x =1+2\cos^{2}x(\color{orange}{\cos^{2}x-1})=1+2\cdot (\color{orange}{-\sin^{2}x})\cos^{2}x=\\
1-\displaystyle\frac{1}{2}\cdot \color{orange}{4\sin^{2}x\cos^{2}x}=1-\displaystyle\frac{1}{2}\color{orange}{\sin^{2}2x}\)

 Krok 6

Stosujemy powyższe obliczenia w naszym przykładzie. Mnożymy przez siebie ułamki i otrzymujemy prawą stronę naszej tożsamości.
\[ \begin{array}{l}
\cdots  = \displaystyle\frac{-4\cos 2x}{\sin^{2} 2x}\cdot \displaystyle\frac{4(1-\displaystyle\frac{1}{2}\sin^{2}2x)}{\sin^{2}2x} =\\
\displaystyle\frac{-16\cos 2x(1-\displaystyle\frac{1}{2}\sin^{2}2x)}{\sin^{4} 2x}=P \quad \quad \blacksquare
\end{array}\]

 Polecenie

Uzasadnij tożsamości trygonometryczne.

 Tożsamość 1

\(\displaystyle\frac{1}{\sin x}-\sin x=\cos x\operatorname{ctg}{x}\)

 Odpowiedź - Dowód

\[ \begin{array}{l}
\displaystyle\frac{1}{\sin x}-\sin x= \\
=\displaystyle\frac{1-\sin^{2} x}{\sin x}
=\displaystyle\frac{\cos^{2} x}{\sin x}=\\
=\displaystyle\frac{\cos x\cdot \cos x}{\sin x}
=\displaystyle\frac{\cos x}{\sin x}\cdot \cos x=\\
=\operatorname{ctg}{x}\cdot \cos x.\quad\quad\quad\blacksquare 
\end{array}\]

 Tożsamość 2

\(\displaystyle\frac{1}{\sin x-1}-\displaystyle\frac{1}{\sin x+1}=\displaystyle\frac{-2}{\cos^{2} x}\)

 Odpowiedź - Dowód

\[ \begin{array}{l}
\displaystyle\frac{1}{\sin x-1}-\displaystyle\frac{1}{\sin x+1}=
\displaystyle\frac{\sin x+1-\sin x+1}{\sin^{2} x-1}=\\
=\displaystyle\frac{2}{\sin^{2} x-1}= \displaystyle\frac{2}{-(1-\sin^{2} x)}=\\
=\displaystyle\frac{-2}{1-\sin^{2} x}= \displaystyle\frac{-2}{\cos^{2} x}. \quad\quad\quad\blacksquare
\end{array}\]