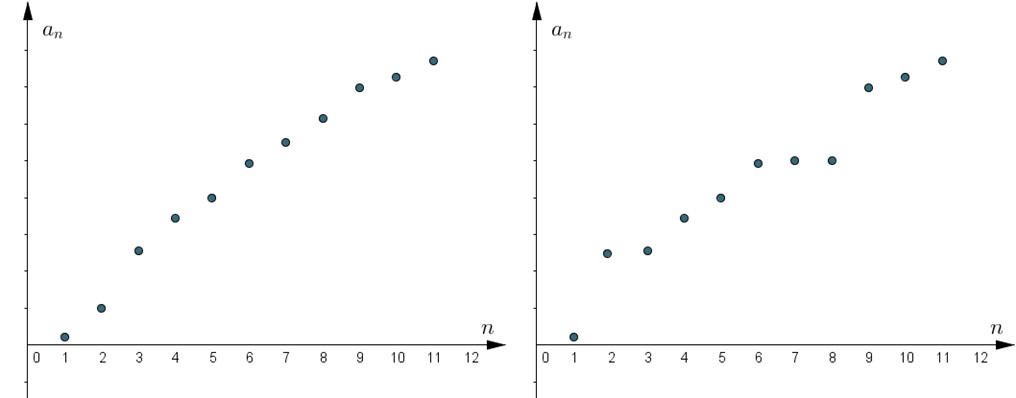
Ciąg \((a_{n})\) jest rosnący, jeżeli każdy kolejny wyraz tego ciągu jest większy od wyrazu poprzedniego, tzn.
\[ \underset{n\in \mathbb{N}}{\huge \forall } a_{n}< a_{n+1}.\]
Jeżeli spełnione jest założenie
\[ \underset{n\in \mathbb{N}}{\huge \forall } a_{n}\leq a_{n+1},\]
wówczas mówimy, że ciąg jest niemalejący.
Przykład ciągu rosnącego i niemalejącego.