Zadanie 5.3.3

Zadanie 5.3.3
Zadanie sprawdzające

Polecenie

Wyznacz punkty nieciągłości funkcji

$f$ oraz określ ich rodzaj.

Wskazówki

Klasyfikacja punktów nieciągłości

I rodzaju

typu "SKOK"

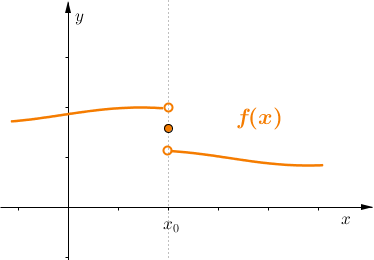
Funkcja ma nieciągłość w punkcie

$x_{0}$ typu "skok", jeśli istnieją granice właściwe lewo i prawostronna w punkcie

$x_{0}$ oraz są sobie różne.
Tzn.

$\displaystyle\lim_{x \to x_{0}^{+}}f(x)=a \ \wedge \ \displaystyle\lim_{x \to x_{0}^{-}}f(x)=b \ \wedge \ a\neq b.$

typu "LUKA"

Funkcja ma nieciągłość w punkcie

$x_{0}$ typu "luka", jeśli istnieją granice właściwe lewo i prawostronna w punkcie

$x_{0},$ mają równe wartości ale są różne od wartości funkcji w punkcie

$x_{0}$ .
Tzn.

$\displaystyle\lim_{x \to x_{0}^{+}}f(x)=a \ \wedge \ \displaystyle\lim_{x \to x_{0}^{-}}f(x)=b \ \wedge \ a=b\neq f(x_{0}).$

II rodzaju

Funkcja ma nieciągłość w punkcie

$x_{0}$ II rodzaju, jeśli co najmniej jedna z granic

$\displaystyle\lim_{x \to x_{0}^{+}}f(x), \ \ \displaystyle\lim_{x \to x_{0}^{-}}f(x)$ nie istnieje lub jest niewłaściwa.

Funkcja 1

$f(x)= \left\{\begin{matrix} \displaystyle\frac{x^{2}\textrm{sgn}x }{x+1},& \textrm{ dla } x\neq -1\\ 0,& \textrm{ dla } x=-1 \end{matrix}\right.$

Rozwiązanie

Algorytm według klasyfikacji punktów nieciągłości

Punktami nieciągłości

$x_{0}$ mogą być jedynie punkty skrajne dziedziny. Wyznaczamy kolejno:

wartość funkcji w punkcie (punktach) $x_{0}$
granicę prawostronną funkcji $f$ w punkcie $x_{0}$
granicę lewostronną funkcji $f$ w punkcie $x_{0}$

Jeżeli

$\displaystyle\lim_{x \to x_{0}^{+}}f(x)=\lim_{x \to x_{0}^{-}}f(x) \neq f(x_{0}),$ to nieciągłość jest I rodzaju typu "LUKA",
$\displaystyle\lim_{x \to x_{0}^{+}} f(x) \neq \lim_{x \to x_{0}^{-}}f(x),$ to nieciągłość jest I rodzaju typu "SKOK",
granice $\displaystyle\lim_{x \to x_{0}^{+}}f(x)$ oraz $\displaystyle\lim_{x \to x_{0}^{-}}f(x)$ nie istnieją lub są niewłaściwe to nieciągłość jest II rodzaju.

Wyznaczamy powyższe wartości w punkcie

$x_{0}=-1:$

$\begin{array}{l} f(-1)=0\\ \displaystyle\lim_{x \to -1^{+}}\frac{x^{2}\textrm{sgn}x }{x+1}=\left [ \frac{-1}{0^{+}} \right ]=-\infty\\ \displaystyle\lim_{x \to -1^{-}}\frac{x^{2}\textrm{sgn}x }{x+1}=\left [ \frac{-1}{0^{-}} \right ]=\infty \end{array}$
Ponieważ granice

$\displaystyle\lim_{x \to x_{0}^{+}}f(x)$ oraz

$\displaystyle\lim_{x \to x_{0}^{-}}f(x)$ są niewłaściwe, zatem jest to nieciągłość II rodzaju.

Poniżej dla zainteresowanych wykres funkcji

$f(x)= \left\{\begin{matrix} \displaystyle\frac{x^{2}\textrm{sgn}x }{x+1},& \textrm{ dla } x\neq -1\\ 0,& \textrm{ dla } x=-1 \end{matrix}\right..$

Funkcja 2

$f(x)= \left\{\begin{matrix} \displaystyle\frac{\cos x}{x},& \textrm{ dla } x \gt 0\\ 2x-1,& \textrm{ dla } x\lt 0 \end{matrix}\right.$

Rozwiązanie

Wyznaczamy wartość funkcji

$f$ w punkcie

$x_{0}=0$ oraz granice lewo i prawostronną w punkcie

$x_{0}=0.$

$\begin{array}{l} f(0)=-1\\ \displaystyle\lim_{x \to 0^{+}}\frac{\cos x}{x}=\left [ \frac{1}{0^{+}} \right ]=\infty\\ \displaystyle\lim_{x \to 0^{-}}\left ( 2x-1 \right )=2\cdot 0-1=-1 \end{array}$
Ponieważ jedna z granic jest niewłaściwa, zatem jest to nieciągłość II rodzaju.

Dla ciekawych wykres funkcji

$f.$

Funkcja 3

Odpowiedź nieprawidłowa

II rodzaju

Odpowiedź nieprawiłdowa

Krok 6 - Odpowiedź

Funkcja

$f(x)= \left\{\begin{matrix} \textrm{ sgn }x,& \textrm{ dla } x \neq 0\\ -1,& \textrm{ dla } x= 0 \end{matrix}\right.$ jest nieciągła w punkcie

$x_{0}=0$ i ma w tym punkcie nieciągłość I rodzaju typu "SKOK".

Dla zainteresowanych wykres funkcji

$f.$

Zadanie 5.3.2